10056. Поиск в
ширину 0 – 1
Задан
неориентированный граф. Вес его ребер может быть равен только значениям 0 или
1. Найдите кратчайшее расстояние между вершинами s и d.
Вход. Первая строка содержит четыре
целых числа: количество вершин n, количество ребер m (n, m ≤ 105) и номера
вершин s и d (1 ≤ s, d ≤ n). Каждая из следующих m
строк содержит три целых числа a, b и w,
задающих неориентированное ребро (a, b) с весом w (0 ≤ w ≤
1).
Выход. Выведите кратчайшее расстояние
между вершинами s и d.
|
Пример
входа |
Пример
выхода |
|
5 5 1 3 1 2 0 2 3 1 3 4 0 4 5 1 1 5 1 |
1 |
РЕШЕНИЕ
поиск в
ширину
Анализ алгоритма
0-1 поиск в
ширину (или 0-1 BFS) – это модификация классического алгоритма поиска в ширину
(BFS), который используется для нахождения кратчайших путей в графах. Отличие
этого алгоритма в том, что веса рёбер в графе могут принимать только значения 0
или 1, что позволяет значительно оптимизировать поиск.
Постановка
задачи. Представим, что у нас есть взвешенный граф, в котором веса
рёбер – это либо 0, либо 1. Например, такой граф можно встретить, когда мы
работаем с городом, в котором некоторые дороги бесплатные (вес 0), а по другим
приходится платить (вес 1). Мы хотим найти кратчайший путь от одной вершины
графа до другой с учётом этих весов.
Проблема
стандартного алгоритма поиска в ширину. Классический алгоритм поиска в
ширину (BFS) имеет оценку сложности O(V + E) и используется для поиска кратчайших
путей в графе, но он подходит только для графов, где все рёбра имеют одинаковый
вес. В случае, если веса рёбер различны, такой подход уже неэффективен – для
этих целей обычно применяют алгоритм Дейкстры с оценкой сложности O(V2 + E) или O(E * log2V). Но для графов
с весами только 0 и 1 существует более быстрый подход – 0-1 BFS.
0-1 BFS Алгоритм
В 0-1 BFS мы используем двустороннюю очередь (deque).
Идея состоит в следующем:
1. Мы начинаем с
исходной вершины start и добавляем её в
очередь с начальным расстоянием, равным 0.
2. При обработке
каждой вершины u (которая извлекается из головы очереди) рассматриваем её
соседей v:
o Если у ребра (u, v) вес 0, то соседняя вершина v помещается в начало
очереди с текущим расстоянием (dist[v] = dist[u]).
o Если у ребра (u, v) вес 1, то соседняя вершина v помещается в конец
очереди с увеличением расстояния на единицу (dist[v] = dist[u] + 1).
3. Это позволяет
эффективно поддерживать правильный порядок обработки вершин: вершины,
достижимые через рёбра с меньшим весом, обрабатываются раньше.
Таким образом, использование двусторонней очереди
гарантирует, что мы всегда имеем доступ к вершине с минимальным расстоянием в
начале очереди, а сложность работы алгоритма остаётся O(V + E).
Релаксация рёбер при 0-1 поиске в ширину похожа на
классическую релаксацию в алгоритме
Дейкстры, но отличается
использованием двусторонней очереди (deque) вместо очереди с приоритетами (priority queue) для упорядочивания вершин на основе веса рёбер.
Алгоритм 0-1 BFS (в отличии от классического BFS) не гарантирует, что каждая вершина будет посещена с
минимальным расстоянием с первого раза, особенно если к одной и той же вершине
можно добраться несколькими путями. Поэтому релаксация рёбер обязательна.
Рассмотрим следующий пример. Инициализируем массив кратчайших
расстояний dist и очередь q:
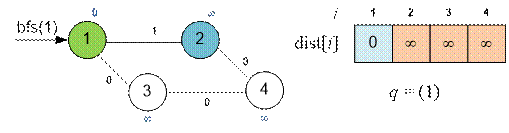
Рассмотрим ребра, исходящие из вершины 1. Релаксируем
ребра (1, 2) и (1, 3). Вершина 3 будет занесена в начало очереди, а вершина 2 в
конец очереди.
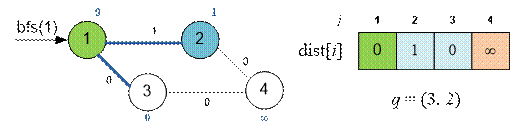
Однако значение dist[2]
= 1 не является
окончательным. Пройдем по ребру 3 – 4 и установим dist[4] = 0, queue = (4, 2). Затем рассмотрим
ребро 4 – 2 и значение dist[2] установится равным 0. Таким образом, dist[2] принимало два
различных значения в результате релаксации (сначала 1, потом 0).
Пример
Граф,
приведенный в примере, имеет вид:
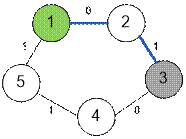
Длина
кратчайшего пути из вершины 1 в 3 равна 1, а сам кратчайший путь имеет вид: 1 –
2 – 3.
Реализация алгоритма
Объявим константу бесконечность.
#define INF
0x3F3F3F3F
Объявим массив кратчайших расстояний dist и список
смежности графа g.
vector<int>
dist;
vector<vector<pair<int, int>>>
g;
Функция bfs реализует поиск в ширину из вершины start.
void bfs(int start)
{
Инициализируем массив кратчайших расстояний dist.
dist = vector<int>(n + 1, INF);
dist[start] = 0;
Объявим очередь и занесем в нее стартовую вершину start.
deque<int> q;
q.push_back(start);
Продолжаем алгоритм поиска в ширину пока очередь не пустая.
while (!q.empty())
{
Извлекаем из головы очереди вершину v.
int v = q.front(); q.pop_front();
Перебираем ребра, исходящие из вершины v.
{
int to = edge.first;
int w = edge.second;
Текущее ребро (v, to) имеет вес w. Проводим его
релаксацию.
if (dist[to] > dist[v] + w)
{
Если ребро релаксирует, то пересчитываем кратчайшее
расстояние dist[to].
dist[to] = dist[v] + w;
В зависимости от веса ребра w добавляем вершину to в конец или в
начало очереди.
if (w == 1)
q.push_back(to);
else
q.push_front(to);
}
}
}
}
Основная часть программы. Читаем входные данные.
scanf("%d %d %d %d",
&n, &m, &s, &d);
g.resize(n + 1);
Читаем граф.
for (i = 0; i < m; i++)
{
scanf("%d
%d %d", &a, &b, &w);
g[b].push_back({ a, w });
}
Запускаем поиск в ширину со стартовой вершины s.
bfs(s);
Выводим кратчайшее расстояние до вершины d.
printf("%d\n",
dist[d]);